NPLM(Neural Probabilistic Language Model)
앞서 "단어가 어떤 순서로 쓰였는가"의 철학으로 만든 모델 n-gram 모델의 문제점은 바로 n을 크게 하면 할 수록 많은 단어들의 history를 확인해야 하는데 만약 예측단계에서 들어온 단어가 history에 등장하지 않은 단어라면 굉장히 자연스러운 문장이 자연스러울 확률이 0이 나오는 대참사가 일어나게 되는 문제점이였다.
정리하면
- 학습 데이터에 존재하지 않는 n-gram이 포함된 문장이 나타날 확률을 0으로 매긴다
- n을 5이상으로 설정하기 어렵기 때문에 문장의 장기 의존성을 포착해내기 어렵다.
- 단어/문장 간 유사도는 고려조차 하지 않는다.
neural net을 쓰기 이전에는 smoothing( 작은 상수를 더해서 0이 안나오도록) 또는 backoff를 사용해서 data sparcity를 해결했다. long-term dependencies 문제는 n개의 토큰만 검색하므로 다음 토큰은 추론할 수 없다는 문제인데 이것을 해결하기 위해 n을 늘리면 또다시 data sparcity와 마주하게 된다. n-gram으로는 long-term dependencies를 해결할 수 없다.
nplm은 이러한 문제점을 해결하는 과정에서 나타났다.
nplm의 학습 과정을 살펴보자
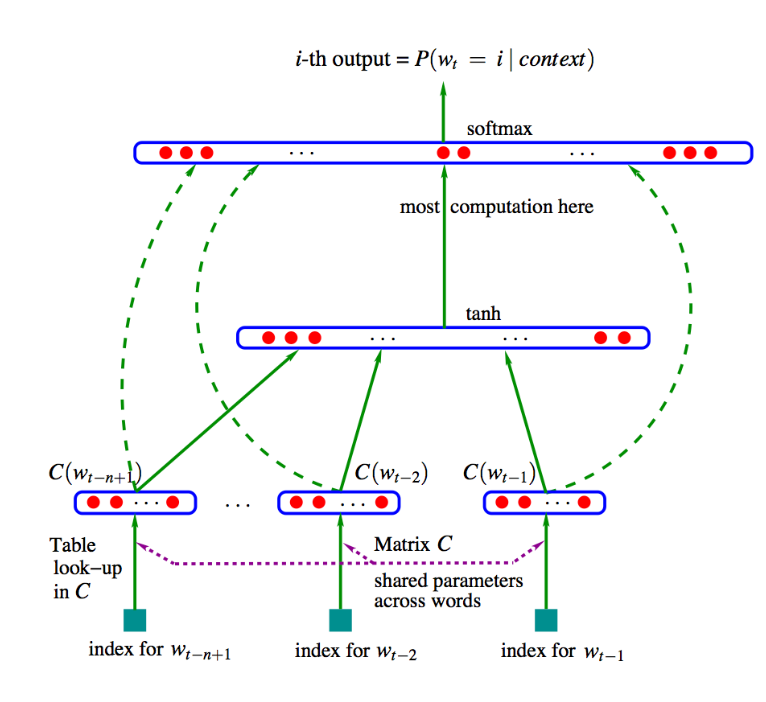
nplm은 단어 시퀀스가 주어졌을때 다음 단어가 무엇인지를 맞추는 과정에 의해 학습된다. 본질은 조건부확률을 이용한 통계량에 있기 때문에 다음 단어가 무엇인지 맞춘다는 말은 아래의 수식을 최대화 한다는 말로 구체화 된다.
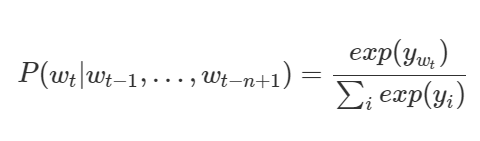
기존의 data sparcity문제, 그러니까 훈련할때 n-gram이 없으면 확률을 0으로 예측하는 문제를 어떻게 nplm은 해결할 수 있을까?
"data sparcity는 왜 생기는가" 를 곰곰히 생각해보면 이산 공간에서 확률을 생각하기 때문이다.
예를 들어 "chasing a llama"라는 n-gram은 흔히 나오는 n-gram이 아니다. 그러나 "chasing a dog/cat"등의 n-gram은 종종 등장한다. 이럴 경우 이산적인 공간에서 생각한다면 당연히 "chasing a llama" 는 확률을 0으로 예측하겠지만 연속적인 벡터공간이라면 다르다.
bi gram을 count base가 아닌 neural network 모델로 구현한다고 하자
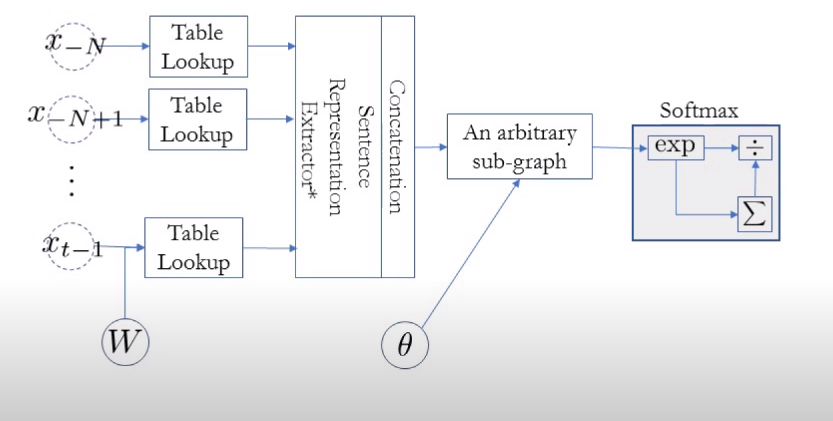
1. there are three teams left for qualification
2. four teams have passed the first round
3. four groups are playing in the feild
훈련 데이터로 위에 세가지 문장이 들어왔다고 하고 테스트할때 "three" 이 들어왔을때 group의 확률을 예측해야한다고 하자. count based라면 당연히 "three group"의 확률은 0이다. 하지만 neural network에서 continuous vecotr space를 사용한다고 하면
1. three teams를 학습할때 teams의 probability를 높이는 방향으로 model이 특정 벡터공간에 three를 매핑할 것이다.

2. four teams 를 학습할때 teams의 probability를 높이기 위해 앞서 1에서 three가 매핑된 곳과 비슷한 곳에 four를 매핑할 것이다. that's optimal behavior
즉, neural network가 "비슷한" n-gram들은 벡터공간에서 가까운 공간에 위치하도록 한다는 것이다. 이때 모델이 판단하는 "비슷"하다는 말의 정의는 n-gram 기반 neural network이기 때문에 n-gram에서 마지막 단어가 비슷하다는 의미이다.

3. four groups가 훈련셋으로 들어왔을 때 모델은 groups가 나올 확률을 높이도록 four를 매핑할 것이다.
그런데 앞서 "four"가 이미 매핑된 곳이 "three"와 비슷한 곳이므로 이제는 "three groups"가 나중에 나오더라도 "three"의 벡터공간 상 위치를 보고 적어도 확률을 0으로 예측하는 것이 아니라 이제는 적어도 "three groups"가
"three teams" 와 비슷한 확률을 예측할 수 있게 된 것이다.

조경현 교수님의 강의를 참조하였습니다
'자연어처리' 카테고리의 다른 글
| 자연어처리(5) - Word2Vec (0) | 2020.02.19 |
|---|---|
| 자연어처리 스터디기록(3)-딥러닝 정리 (0) | 2020.02.08 |
| 자연어처리 스터디 기록(2)-임베딩의 의미 (0) | 2020.01.27 |
| 자연어처리 스터디 기록(1)-임베딩 (0) | 2020.01.23 |



